Perhitungan dan Pembahasan Tegangan Normal Pada Penampang Annular

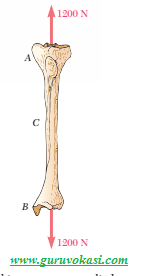
Sebuah alat pengukur regangan (strain gauge) diletakkan pada titik C pada permukaan tulang AB. Diketahui ketika tulang tersebut mengalami gaya sebesar 1200 N Strain Gauge menunjukkan nilai rata-rata tegangan normal sebesar 3,80 MPa,. Jika diasumsikan penampang pada titik C menjadi annular dan diameter luarnya sebesar 25 mm, maka berapakah besar diameter dalam pada titik C?\begin{aligned}P &=& \ 1200\ N\\ \sigma &=& \ 3,80\ MPa\\d_2 &=& \ 25\ mm\end{aligned} Ditanya diameter dalam (d1) pada point C ?
Guru Menjawab \begin{aligned} \sigma=\frac{P}{A}\therefore\ A=\frac{P}{\sigma}\end{aligned} \begin{aligned} A\ &=&\ \frac{\pi}{4}\left(d_1^2-d_2^2\right)\\d_1^2 & = & d_2^2-\frac{4A}{\pi}\\ & = & d_2^2-\frac{4P}{\pi\sigma}\\ & = & \left({25\ x10}^{-3}\right)^2-\frac{4\left(1200\right)}{\pi\left(3,80\ {x\ 10}^6\right)}\\d_1^2 &=& 222,9\ x{10}^{-6}m^2\\ d_1 & = & \sqrt{222,9\ x{10}^{-6}m^2}\\ d_1 & = &14\ mm\end{aligned}