Pengertian, Rumus, dan Sifat-sifat Notasi Sigma dan Induksi Matematika

Notasi Sigma

Dalam matematika notasi sigma dilambangkan sebagai berikut “∑”, lambang ini berasal dari huruf yunani yang artinya adalah penjumlahan. Untuk simbol lengkap dari  notasi sigma adalah $$\sum_{B,B}^{B,\ A}RUMUS$$ dengan B,B adalah Batas Bawah dan B,A adalah batas atas. Jadi notasi sigma ini diperlukan untuk menyatakan penjumlahan suku-suku suatu barisan bilangan yang disebut deret bilangan. Aturan suku-suku barisan bilangan dinyatakan dengan rumus notasi sigma. Suku awal dimulai dimulai dari batas bawah dan suku terakhir dari batas atas pada notasi sigma. Domain dari batas bawah sampai dengan batas atas adalah bilangan bulat yang berurutan.

Contoh:

$$\sum_{i=1}^{6}{2i\ dibaca\ "sigma\ dari\ 2i\ sengan\ i\ mulai\ dari\ 1\ sampai\ dengan\ 6"}$$

$$i \ = \ 1 \ disebut \ batas \ bawah$$

$$i \ = \ 6 \ disebut \ batas \ bawah$$

$$i \ = \ {1,2,3,4,5,6}$$

Menguraikan Notasi Sigma dan Hasilnya

\begin{aligned}\sum_{i=1}^{n}{U_i=U_1+U_2+U_3+\ ...\ \ +U_n} \\ \sum_{i=1}^{6}{2_i=\left(2\ \bullet1\right)+\left(2\ \bullet2\right)+\left(2\ \bullet3\right)+\ \left(2\ \bullet4\right)\ +\left(2\ \bullet5\right)+\left(2\ \bullet6\right)} \\ =\left(2\right)+\left(4\right)+\left(6\right)+\ \left(8\right)\ +\left(10\right)+\left(12\right) \\=\ 42\end{aligned}

Menyatakan Suatu Penjumlahan dengan Notasi Sigma

Menyatakan Suatu Penjumlahan dengan notasi sigma
Jika pada penjelasan diatas kita menguraikan notasi sigma menjadi bentuk penjumlahan (deret bilangan), maka berikut ini akan dijelaskan cara agar bentuk penjumlahan (deret bilangan) menjadi notasi sigma:
2.(1) + 2.(2) + 2.(3) +2.(4)+2.(5)+2.(6)
Cara agar bentuk penjumlahan (deret bilangan) diatas dijadikan notasi sigma adalah:

1. Menentukan rumus notasi sigma, yaitu dengan melihat angka yang konstan yaitu anhka 2 dan angka yang bertambah  yaitu 1,2, …,6, maka rumus notasi sigma ada;ah 2i.
2. Menentukan batas bawah dan batas atas, yaitu dengan melihat angka yang bertambah dimulai dari 1 dan berakhir sampai angka 6, maka $$\sum\frac{6}{i=1}$$.

Jadi Notas Sigma Untuk soal diatas dapat dirinci diringkas sebagai berikut $$2.(1)\ +\ 2.(2)\ +\ 2.(3)\ +2.(4)+2.(5)+2.(6)=\sum_{i=1}^{6}2i$$.

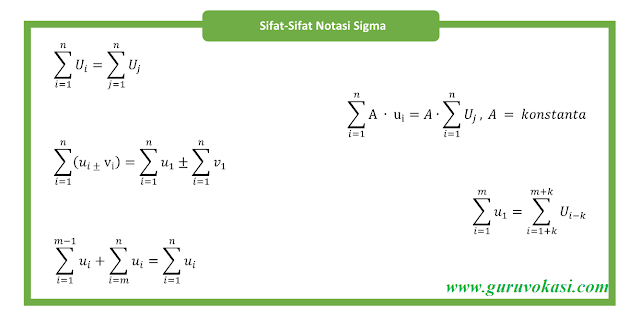
Sifat-Sifat Notasi Sigma
Dalam notasi sigma terdapat beberapa sifat yang harus kita hafal, agar memudahkan kita dalam mengerjakan soal terkait notasi sigma:

1. $$\sum_{i=1}^{n}{U_i=\sum_{j=1}^{n}U_j}$$
2. $$\sum_{i=1}^{n}{{A\bullet U}_i=A\bullet\sum_{i=1}^{n}U_j},\ A\ =\ konstanta$$
3. $$\sum_{i=1}^{n}\left(u_i\pm v_i\right)=\sum_{i=1}^{n}u_1\pm\sum_{i=1}^{n}v_1$$
4. $$\sum_{i=1}^{m}u_1=\sum_{i=1+k}^{m+k}U_{i-k}$$
5. $$\sum_{i=1}^{m-1}u_i+\sum_{i=m}^{n}{u_i=\sum_{i=1}^{n}u_i}$$

Induksi Matematika
Induksi matematika merupakan cara untuk membuktikan kebenaran sebuah rumus, bilangan yang digunakan untuk membuktikan induksi matematika adalah bilangan asli. Jika anda ingin membuktikan suatu rumus P(n) berlaku untuk semua n bilangan asli, maka langkah-langkahn nya adalah sebagai berikut ini:

1. Dibuktikan bahwa P(n) benar untuk n = 1
2. Jika P(k) benar maka n= k, maka dibuktikan bahwa P(n) benar n=k+1

Terimakasih telah berkunjung pada website kami, seperti pepatah kuni mengatakan tiada gading yang tak retak kami berharap teman-teman sekalian mamu memberikan kritik dan saran untuk memperbaiki kekurangan website kami.