Petunjuk B Soal terdiri dari tiga bagian, yaitu pernyataan, kata sebab, dan alasan yang disusun berurutan.
Pilihlah:
A. Jika pernyataan benar, alasan benar, dan keduanya menunjukkan hubungan sebab akibat.
B. Jika pernyataan benar dan alasan benar, tetapi keduanya tidak menunjukkan hubungan sebab akibat.
C. Jika pernyataan benar dan alasan salah.
D. Jika pernyataan salah dan alasan benar.
E. Jika pernyataan dan alasan keduanya salah.
Petunjuk C Pilihlah:
A. Jika (1), (2), dan (3) yang benar.
B. Jika (1) dan (3) yang benar.
C. Jika (2) dan (4) yang benar.
D. Jika hanya (4) yang benar
E. Jika semuanya benar.
TES KEMAMPUAN & POTENSI AKADEMIK
- Jika akar-akar 3x² + a x - 3 = 0 dan 2x² + 6x + 3b = 0 saling berkebalikan maka b- a = ....
- Jika A²ˣ → 2 maka (A⁵ˣ - A⁻⁵ˣ) : (A³ˣ - A⁻³ˣ)
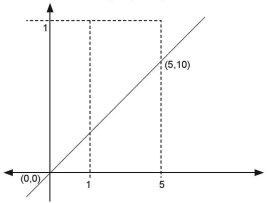
- Suatu garis yang melalui titik (0, 0) membagi persegi panjang dengan titik-titik sudut (1, 0), (5, 0), (1, 12), dan (5, 12) menjadi dua bagian yang sama luas. Gradien garis tersebut adalah …
- Soal
- Jika grafik fungsi y = x² -(9 + a) x + 9a diperoleh dari grafik fungsi y = x² - 2x – 3 melalui pencerminan terhadap garis x = 4 maka a = ....
- Tujuh finalis lomba menyanyi tingkat SMA di suatu kota berasal dari 6 SMA yang berbeda terdiri atas empat pria dantiga wanita. Diketahui satu pria dan satu wanita berasal dari SMA “A” tidak tampil berurutan, maka susunan urutan tampil yang mungkin ada sebanyak ....
- Jika fungsi f(x) = 2x + a +b dan g(x) = bx +1 memenuhi (f◦g)(x) = 2(g(x)) maka a+ b =
- Jika fungsi f dan g mempunyai invers dan memenuhi g(x - 2) = f (x + 2), maka g⁻¹(x) = . ..
- Diketahui matriks $$A=\left(\begin{matrix}3&4\\1&2\\\end{matrix}\right)\ B=\left(\begin{matrix}3&2\\p&2\\\end{matrix}\right)\ dan\ C=\left(\begin{matrix}1&1\\2&q\\\end{matrix}\right).\ Jika\ det\ \left(AB\right)=det\left(2C\right),\ maka\ p+q\ =$$
- Jika alog(b-2), alog(b), dan alog(b+ 4) adalah tiga suku berurutan suatu barisan aritmatika dan jumlah tiga suku tersebut adalah 6, maka 2a + b = ....
- Perhatikan gambar di bawah ini!
- Nilai ujian matematika 30 siswa pada suatu kelas berupa bilangan cacah tidak lebih daripada 10. Rata-rata nilai mereka adalah 8 dan hanya terdapat 5 siswa yang memperoleh nilai 7. Jika p menyatakan banyak siswa yang memperoleh nilai kurang dari 7 maka nilai p terbesar yang mungkin adalah ....
- $$Diketahui\ f\left(x\right)=x^2+ax+b\ ,\ jika\ \frac{\lim}{x\rightarrow\ -2}{\frac{x+2}{f\left(x\right)}=-\frac{1}{5}\ maka\ a+b\ adalah\ ....}\ $$
- Jika 2x - y =-1,3x - 2y = -3,ax - 2y = 4b, dan 4x - a y = 2b, maka a+b =....
- Semua bilangan real x yang memenuhi $$\frac{x^2+1}{\left|x\right|-1}\geq\ x$$ adalah
A. -7
B. -5
C. 5
D. 6
E. 7
Pembahasan
3x² + ax - 3 = 0 dan 2x² + 6x - 3b = 0 saling
berkebalikan maka didapat:
-a =6 → a = -6
-3b =3 → a = -1
Jadi , b- a = -1-(-6) = 5
B. -5
C. 5
D. 6
E. 7
Pembahasan
3x² + ax - 3 = 0 dan 2x² + 6x - 3b = 0 saling
berkebalikan maka didapat:
-a =6 → a = -6
-3b =3 → a = -1
Jadi , b- a = -1-(-6) = 5
A. 31/18
B. 31/9
C. 32/18
D. 33/9
E. 33/18
Pembahasan
B. 31/9
C. 32/18
D. 33/9
E. 33/18
Pembahasan
\begin{aligned}A^{2x}&=&2\\ A^x&=&\sqrt2\\ \frac{A^{5x}-A^{-5x}}{A^{3x}+A^{-3x}}&=&\frac{A^{5x}-\frac{1}{A^{5x}}}{A^{3x}+\frac{1}{A^{3x}}}\\ &=&\frac{\frac{\left(A^{5x}\right)^2-1}{A^{5x}}}{\frac{\left(A^{3x}\right)^2+1}{A^{3x}}}\\ &=&\frac{\left(A^{5x}\right)^2-1}{A^{5x}}x\frac{A^{3x}}{\left(A^{3x}\right)^2+1}\\ &=&\frac{\left(A^{5x}\right)^2-1}{A^{2x}\left(\left(A^{3x}\right)^2+1\right)}\\ &=&\frac{\left(A^{2x}A^{2x}A^x\right)^2-1}{A^{2x}\left(\left(A^{2x}A^x\right)^2+1\right)}\\ &=&\frac{\left(2\bullet2\bullet\sqrt2\right)^2-1}{2\left(\left(2\bullet\sqrt2\right)^2+1\right)}\\ &=&\frac{31}{18} \end{aligned}
A. ½
B. 1
C. 2
D. 12/5
E. 3
Pembahasan
L persegi panjang 12 x 4 = 48 satuan luas
½ luas persegi panjang = luas trapesium = 24
satuan luas
jumlah sisi sejajar = a + b =12
diasumsikan a = 2 dan b = 10
maka gradien = 10 - 0 / 5 -0 = 10/5 =2
B. 1
C. 2
D. 12/5
E. 3
Pembahasan
L persegi panjang 12 x 4 = 48 satuan luas
½ luas persegi panjang = luas trapesium = 24
satuan luas
jumlah sisi sejajar = a + b =12
diasumsikan a = 2 dan b = 10
maka gradien = 10 - 0 / 5 -0 = 10/5 =2
Semua nilai x yang memenuhi (3/x)-(3/x+3) ≥ 0 adalah ….
A. x < 0
B. -3 < x < 0
C. -3 < x < 0
D. x < -3 atau x > 0
E. x <-3 atau x > 0
B. -3 < x < 0
C. -3 < x < 0
D. x < -3 atau x > 0
E. x <-3 atau x > 0
Pembahasan
\begin{aligned}\frac{3}{x}-\frac{3}{x+3}\geq0\\ \frac{3x+9}{x(x+3)}-\frac{3x}{x(x+3)}\geq0\\ \frac{9}{x^2+3}\geq0\end{aligned} Syarat ≠-3
Pembuat nol penyebut
x²+3x =0
x=0 dan x = -3 garis bilangan
Pembuat nol penyebut
x²+3x =0
x=0 dan x = -3 garis bilangan
A. 7
B. 5
C. 3
D. -5
E. -7
Pembahasan
P(x,y) → P’ (2a -x’,y’), a = 4
x = 2a – x’
= 2(4) – x’
= 8-x’
y = y’
Substitusi x dan y ke y = x2 - 2x – 3
sehingga:
B. 5
C. 3
D. -5
E. -7
Pembahasan
P(x,y) → P’ (2a -x’,y’), a = 4
x = 2a – x’
= 2(4) – x’
= 8-x’
y = y’
Substitusi x dan y ke y = x2 - 2x – 3
sehingga:
y ' = (8- x')2 - 2(8- x')- 3
y = x2 -14x + 45
maka:
x2 -(9 + a)x + 9a = x2 -14x + 45
sehingga didapat 9a = 45 → a = 5
y = x2 -14x + 45
maka:
x2 -(9 + a)x + 9a = x2 -14x + 45
sehingga didapat 9a = 45 → a = 5
A. 144
B. 108
C. 72
D. 36
E. 35
B. 108
C. 72
D. 36
E. 35
dengan menggunakan permutasi maka kemungkinan banyaknya urutan 7 finalis yang terdiri atas 4 pria dan 3 wanita:\begin{aligned}P_4^4+P_3^3&=&4!x3!\\ &=&\left(4x3x2x1\right)x\left(3x2x1\right)\\ &=&24x6\\ &=&144\ cara\end{aligned} kemudian diketahui 1 pria dan 1 wanita dari SMA A tidak tampil berurutan maka kemungkinan urutannya:
\begin{aligned} 6xP_3^3xP_2^2&=&6\ x\ 3!\ x\ 2!\\ &=&6\ x\ 6\ x\ 2\\ &=&72 \end{aligned}Jadi, banyaknya susunan yang mungkin adalah 144- 72 = 72 cara
A. -2
B. -1
C. 0
D. 1
E. 2
Pembahasan
f(x) = 2x + a + b
g(x) = bx +1
(f◦g)(x) = 2(g(x))
(f◦g)(x) = 2(bx + 1) +a + b = 2bx + 2 + a + b
2x(g(x)) = 2 (bx + 10 = 2bX + 2
2bx + 2 + a + b = 2bx + 2
a + b = 0
B. -1
C. 0
D. 1
E. 2
Pembahasan
f(x) = 2x + a + b
g(x) = bx +1
(f◦g)(x) = 2(g(x))
(f◦g)(x) = 2(bx + 1) +a + b = 2bx + 2 + a + b
2x(g(x)) = 2 (bx + 10 = 2bX + 2
2bx + 2 + a + b = 2bx + 2
a + b = 0
A. f⁻¹(x) + 4
B. 4 - f-1(x)
C. f⁻¹(x + 4)
D. -f¹(x)- 4
E. f⁻¹(x)- 4
Pembahasan
g(x – 2 ) = f(x + 2)
g(x) – 2 = f(x) + 2
g(x) = f(x) + 4
f(x) = g (x) -4
g⁻¹ (x) = f⁻¹ (x) -4
B. 4 - f-1(x)
C. f⁻¹(x + 4)
D. -f¹(x)- 4
E. f⁻¹(x)- 4
Pembahasan
g(x – 2 ) = f(x + 2)
g(x) – 2 = f(x) + 2
g(x) = f(x) + 4
f(x) = g (x) -4
g⁻¹ (x) = f⁻¹ (x) -4
A. 4
B. 5
C. 6
D. 7
E. 8
Pembahasan
B. 5
C. 6
D. 7
E. 8
Pembahasan
$$AB=\left(\begin{matrix}3&4\\1&2\\\end{matrix}\right)\left(\begin{matrix}3&2\\p&2\\\end{matrix}\right)=\left(\begin{matrix}9+4p&14\\3\ +\ 2p&6\\\end{matrix}\right)$$ det(AB) = (9 + 4p)(6)-(3 + 2p)(l4)
= 54+ 24p- 42- 28p
=12- 4p $$2C=2\left(\begin{matrix}1&1\\2&q\\\end{matrix}\right)=\left(\begin{matrix}2&2\\4&2q\\\end{matrix}\right)$$
= 54+ 24p- 42- 28p
=12- 4p $$2C=2\left(\begin{matrix}1&1\\2&q\\\end{matrix}\right)=\left(\begin{matrix}2&2\\4&2q\\\end{matrix}\right)$$
det(2C) = 4q- 8
det(AB) = det(2C)
12- 4p = 4q- 8
-4p-4q=-8-12
4p+ 4q = 20
p+ q = 5
A. 6
B. 7
C. 8
D. 9
E. 10
B. 7
C. 8
D. 9
E. 10
Pembahasan
S₃ = 3/2 (ªlog(b- 2) + ªlog(b+4))
6 = 3/2 (ªlog(b- 2)(b+4))
4 = ªlog(b-2)(b+ 4)
a4 = (b-2)(b+ 4)
maka a = 2 dan b = 4
sehingga 2a + b = 2(2)+ 4 = 8
S₃ = 3/2 (ªlog(b- 2) + ªlog(b+4))
6 = 3/2 (ªlog(b- 2)(b+4))
4 = ªlog(b-2)(b+ 4)
a4 = (b-2)(b+ 4)
maka a = 2 dan b = 4
sehingga 2a + b = 2(2)+ 4 = 8
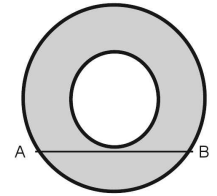
Diketahui dua buah lingkaran dengan titik pusat yang sama, berturut-turut berjari-jari R1 dan R2 dengan R1 >R2 . Jika panjang tali busur AB = 10 cm maka selisih luas lingkarang tersebut adalah ... cm²
A. 10𝞹
B. 15𝞹
C. 20𝞹
D. 25𝞹
E. 30𝞹
Pembahasan\begin{aligned} R_1&>&R_2\\ AB>\frac{10}{2}&=&5=\left(R_1-R_2\right)^2\\L_1-L_2&=&\left(\pi R_1^2\right)-\left(\pi R_1^2\right) \\ &=&\pi\left(R_1-R_2\right)^2\\ &=&\pi\left(5\right)^2\\ &=&25\pi \end{aligned}
B. 15𝞹
C. 20𝞹
D. 25𝞹
E. 30𝞹
Pembahasan\begin{aligned} R_1&>&R_2\\ AB>\frac{10}{2}&=&5=\left(R_1-R_2\right)^2\\L_1-L_2&=&\left(\pi R_1^2\right)-\left(\pi R_1^2\right) \\ &=&\pi\left(R_1-R_2\right)^2\\ &=&\pi\left(5\right)^2\\ &=&25\pi \end{aligned}
A. 5
B. 7
C. 9
D. 11
E. 14
Pembahasan
Misalkan, a = nilai x di mana x adalah siswa
a ≤ 10 \begin{aligned}{\overline{x}}_{30}=8\rightarrow\sum{x_{30}=240}\\ {\overline{x}}_5=7\rightarrow\sum{x_5=35}\\ \sum{x_{25}=240\ -35\ =205}\end{aligned} p siswa yang mempunyai a < 7; q siswa yang mempunyai a > 7
maka didapat:
p+ q = 25
Σp + Σq = 205
kita asumsikan a terbesar 10 dan a terkecil 6 kemungkinan banyaknya p dan q paling mendekati jumlah 205: p =11 dan q =14
bukti:
Σp + Σq = 6(11) + 10(14) =206
B. 7
C. 9
D. 11
E. 14
Pembahasan
Misalkan, a = nilai x di mana x adalah siswa
a ≤ 10 \begin{aligned}{\overline{x}}_{30}=8\rightarrow\sum{x_{30}=240}\\ {\overline{x}}_5=7\rightarrow\sum{x_5=35}\\ \sum{x_{25}=240\ -35\ =205}\end{aligned} p siswa yang mempunyai a < 7; q siswa yang mempunyai a > 7
maka didapat:
p+ q = 25
Σp + Σq = 205
kita asumsikan a terbesar 10 dan a terkecil 6 kemungkinan banyaknya p dan q paling mendekati jumlah 205: p =11 dan q =14
bukti:
Σp + Σq = 6(11) + 10(14) =206
A. 7
B. 5
C. 1
D. -1
E. -7
Pembahasan \begin{aligned} \frac {\lim}{x\ \rightarrow2}{\frac{x+\ 2}{f\left(x\right)}=-\frac{1}{5}}\\ \frac{\lim}{x\ \rightarrow2}{\frac{x+\ 2}{x^2+ax+b}=-\frac{1}{5}}\\ \frac{\lim}{x\ \rightarrow2}{\frac{x+\ 2}{x^2+ax+b}=-\frac{1}{5}}\\ \frac{\lim}{x\ \rightarrow2}{\frac{x+\ 2}{\left(x+2\right)\left(x+q\right)}=-\frac{1}{5}} \end{aligned} didapat p = 2 dan q = -5 + 2 = -3
sehingga a = -1 dan b = -6
a + b = -7
B. 5
C. 1
D. -1
E. -7
Pembahasan \begin{aligned} \frac {\lim}{x\ \rightarrow2}{\frac{x+\ 2}{f\left(x\right)}=-\frac{1}{5}}\\ \frac{\lim}{x\ \rightarrow2}{\frac{x+\ 2}{x^2+ax+b}=-\frac{1}{5}}\\ \frac{\lim}{x\ \rightarrow2}{\frac{x+\ 2}{x^2+ax+b}=-\frac{1}{5}}\\ \frac{\lim}{x\ \rightarrow2}{\frac{x+\ 2}{\left(x+2\right)\left(x+q\right)}=-\frac{1}{5}} \end{aligned} didapat p = 2 dan q = -5 + 2 = -3
sehingga a = -1 dan b = -6
a + b = -7
A. 0
B. 1
C. 2
D. 3
E. 4
Pembahasan
2x - y = -1 | x3 | 6x - 3y = -3
3x - 2y = -3 |x2 | 6x - 4y = -6 _
y = 3
dengan substitusi didapat 2x - 3 = -1 x =1
Subtitusi x dan y ke ax - 2y = 4b dan 4x - ay = 2b
didapat persamaan baru:
untuk ax - 2y = 4b a - 4b = 6
untuk 4x - ay = 2b 3a + 2b = 4
B. 1
C. 2
D. 3
E. 4
Pembahasan
2x - y = -1 | x3 | 6x - 3y = -3
3x - 2y = -3 |x2 | 6x - 4y = -6 _
y = 3
dengan substitusi didapat 2x - 3 = -1 x =1
Subtitusi x dan y ke ax - 2y = 4b dan 4x - ay = 2b
didapat persamaan baru:
untuk ax - 2y = 4b a - 4b = 6
untuk 4x - ay = 2b 3a + 2b = 4
A. -1< x < 0 atau 0 < x <1
B. x < 0
C. -1< x < 1
D. x < -1 atau x >1
E. x <-1
B. x < 0
C. -1< x < 1
D. x < -1 atau x >1
E. x <-1
Pembahasan
\begin{aligned}\frac{x^2+1}{\left|x\right|-1}&&\geq\ x\\ \frac{x^2+1}{\left|x\right|-1}-x&&\geq0\\ \frac{x^2+1}{\left|x\right|-1}-\frac{x\left|x\right|-1}{\left|x\right|-1}&&\geq0\\ \frac{x^2-x\ \left|x\right|+2}{\left|x\right|-1}&&\geq0\\x\neq-1\ dan\ x\ &&\neq1\\ x<-1\ &&dan\ x\ >1\end{aligned}
LATIHAN SOAL TPA SBMPTN SAINTEK LAINNYA









Tidak ada komentar:
Posting Komentar